현실의 문제는 해가 정확히 1개가 존재하는, 유일한 해가 있는 방정식으로 풀기 어려운 것이 대부분입니다. 따라서, 우리는 정확히 매칭되는 정답이 아닌, 근사해(approximated solution)를 구해야합니다. 근사해를 구하기 위해 우리는 최소자승법 (또는 최소제곱법)을 적용하여 회귀분석을 하고, 식을 얻을 수 있습니다. (최소자승법은 영어로 Least Squares Method, Least squares,Least squaresapproximation라고 할 수 있습니다.)
최소 제곱법에서 근사해를 구하는 것은 아래의 3가지와 같습니다.
- 해가 정확히 일치하지는 않지만, 실제값과의 차이가 별로 나지 않는 해를 구하는 것
- 실제값과 예측값의 오차가 최소화되는 것
- 실제값과 가장 가까운 예측값을 구하는 것
수학적으로 최소제곱법을 설명해보면, 회귀분석에서 과결정계(overdetermined systems)* 의 경우에 근사해를 구하기 위해 모든 데이터에 대한 잔차* 의 제곱의 합이 최소화되도록 회귀식과 그의 해(solution)를 구하는 것입니다. 따라서, 최소제곱법은 회귀모델의 파라미터 추정을 위한 최적화 알고리즘이라고도 할 수 있습니다. 쉽게 말해서, 가지고 있는 데이터셋에 가장 fit한 모델(함수)의 파라미터를 조정하여 얻어내는 것이고, fit하다는 것의 기준은 잔차가 0에 가까워지는 것입니다. 정확히는 잔차 제곱의 합(the sum of squared residuals)이 0에 가까워지도록 계산합니다.
* 과결정계 : 미지수보다 방정식의 수가 더 많은 연립방정식
* 잔차 : 실제값과 모델의 예측값의 차이
최소제곱법은 선형 최소제곱(Linear Least Squares), 비선형 최소제곱(Non-Linear Least Squares)이 있습니다. 직선모델인 선형 회귀분석을 하는 경우에 선형 최소제곱법으로 매개변수(parameter)를 조절하게 되고, 지수함수, 로지스틱 함수, 다항식 등의 비선형 회귀분석을 하는 경우에는 비선형 최소제곱법으로 그에 맞는 알고리즘(경사 하강법이나 레벤버그-마콰르트 알고리즘 등)으로 매개변수를 조절하게 됩니다. 머신러닝 분야에서 데이터를 선형회귀모델에 학습시키는 경우로 예를 들어 설명해보겠습니다.


위의 그래프처럼 모든 점들을 정확히 지나는 직선을 구할 수 없기 때문에, 최대한 실제 점들과 선의 거리가 최소화되는 선형회귀식의 해를 구하고자 합니다.
* 해당 글에서는 다소 간단한 Ax = b 식을 기준으로 설명을 진행하겠습니다.
위의 선형회귀식에서
- A는 m*n행렬로 n개의 feature를 가진 데이터가 m개 있는 형태입니다.
- x벡터의 형태는 A의 각 feature마다 곱해지는 가중치 파라미터를 원소로 가지는 n*1크기 벡터입니다.
- b벡터의 형태는 Ax를 곱해서 나오는 결과로 m*1크기 벡터입니다.
- 만약 데이터에 노이즈(잡음)이 큰 경우, y라는 편향값(random noise)도 식에 추가하여 해를 구하게 됩니다.
결국, 위의 식은 b를 구하기 위한 A에 대한 선형회귀식이며, x가 바로 최소제곱법에서 구해야하는 목표입니다. 이러한 이유로 x벡터를 최소제곱해(Least Squares Solution)라고 부릅니다.
본격적으로 최소제곱법을 적용하여 x를 구해주기 위해 A, x, b는 아래의 3가지 조건들을 만족해야합니다.

- 1번의 의미는 A의 열벡터가 모두 선형 독립이어야 한다는 것입니다.
- 2번의 의미는 A의 열벡터로 생성된 A의 열공간에는 Ax라는 벡터가 항상 존재한다는 의미입니다.
- 3번의 의미는 C(A)내에 속하는 어떠한 벡터의 선형결합으로도 b 벡터를 만들 수 없다는 의미입니다. 이는 위의 그래프 그림에서 직선에 위에 b가 없는 모습과 연결됩니다.
위의 조건에 따라 정확히 b라는 값을 구할 수 없기 때문에 b에 근사한 b^ (비 햇)을 구하게 됩니다. b^는 선형회귀식에 따라 Ax^와 같습니다.

따라서, 저희는 b와 b^의 차이가 최소가 되는 x^를 찾아야합니다. 이는 || b - Ax^ || 이 최소값이 되는 x^를 구하는 것으로 풀어낼 수 있습니다. || b - Ax^ || 는 2-norm값으로, b와 b^ 두 벡터의 거리를 계산하는 것입니다.
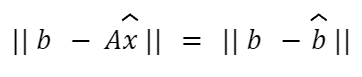
* 해당 식의 꼴에는 제곱근의 형태가 있기 때문에, 추후 미분을 활용하여 해를 구하는데에 어려움이 있습니다. 이는 해석학적 방법의 계산으로 norm에 제곱을 해준 값을 사용해주게 됩니다. 자세한 이야기는 기회가 된다면 다음에 다뤄보겠습니다.
직선위에 있는 임의의 점 Ax^가 b와 제일 가깝기 위해서는 b를 직선에 수직(90°)으로 정사영시킨 것이 Ax^여야 합니다. 따라서, b에 대한 정사영인 Ax^일 때가 잔차의 최솟값이며, 결국 x^가 최소제곱해가 됩니다. 이러한 원리를 통해 최소제곱해를 구해주는 계산과정에 정사영 행렬을 이용하게 됩니다. 이와 연관된 방정식으로는 Normal Equation이 있습니다. 정사영된 벡터와 90도 수직을 이룬다는 성질 + 수직을 이루는 두 벡터의 내적값은 0이 된다는 성질을 통해 Normal Equation을 도출해낼 수 있습니다.
* 자세한 설명은 아래의 사진의 설명으로 대체하였습니다.



정리
1) 최소제곱법이 무엇인가
2) 해를 구하는 구체적인 방법 (대수적 방법)
* 편미분을 이용하는 해석적 방법도 있으나 해당 글에서는 다루지 않았습니다.
3) 이를 통해 도출되는 정사영 행렬
참고 자료
1) Linear Algebra and Its Applications 5th Edition, David C.Lay, Pearson Education (2016)
- Section 6.5 Least Squares Problems
2) https://youtu.be/B_WZdmCGqBc?si=h4NsYCgV0w_cTPWX
'Mathematics > Linear Algebra' 카테고리의 다른 글
| Norm이란? L1 Norm, L2 Norm 설명 (0) | 2023.09.11 |
|---|---|
| [칸아카데미] 모두를 위한 선형대수학 - (28) 열공간의 차원, 기저 열과 축열의 관계, 후보 기저의 A의 열공간 생성 (1) | 2023.04.04 |
| [칸아카데미] 모두를 위한 선형대수학 - (27) 영공간의 차원 (0) | 2023.03.12 |
| [칸아카데미] 모두를 위한 선형대수학 - (26) 어떠한 부분간의 기저도 원소의 수가 같습니다. (0) | 2023.03.12 |
| [칸아카데미] 모두를 위한 선형대수학 - (25) R3에 있는 열공간을 평면으로 시각화하기 (0) | 2022.12.29 |