1. 검증 데이터셋을 활용한 머신러닝 모델 학습
- 기존의 학습, 평가 데이터셋으로만 진행하던 것에서 검증데이터셋을 추가하여 학습의 정확도를 높히는 방법
- 학습된 모델을 중간점검하는 느낌
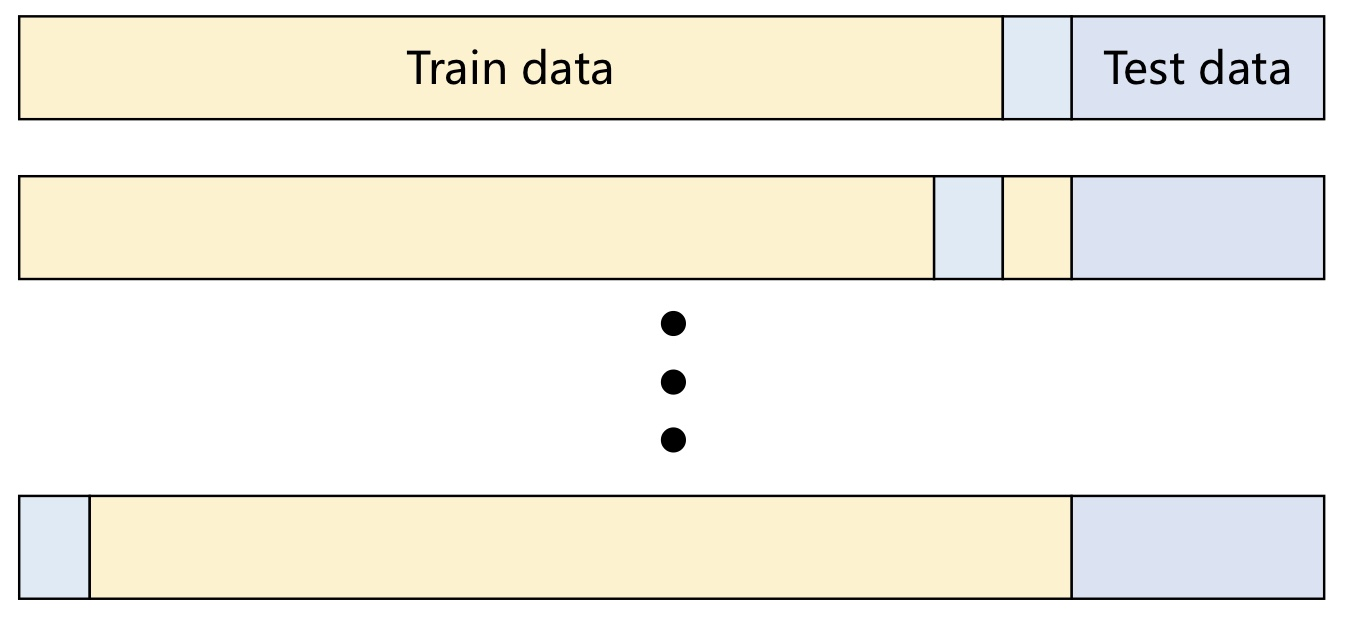
# LOOCV (Leave One Out Cross Validation) 방법론
- 모든 학습 데이터 샘플 1개마다 검증하는 방법
- (오직 한개의 데이터 샘플로만 검증하는 것은 편향된 결과를 주기 때문)
- 모든 데이터로 검증하기 때문에 계산량이 매우 높아짐
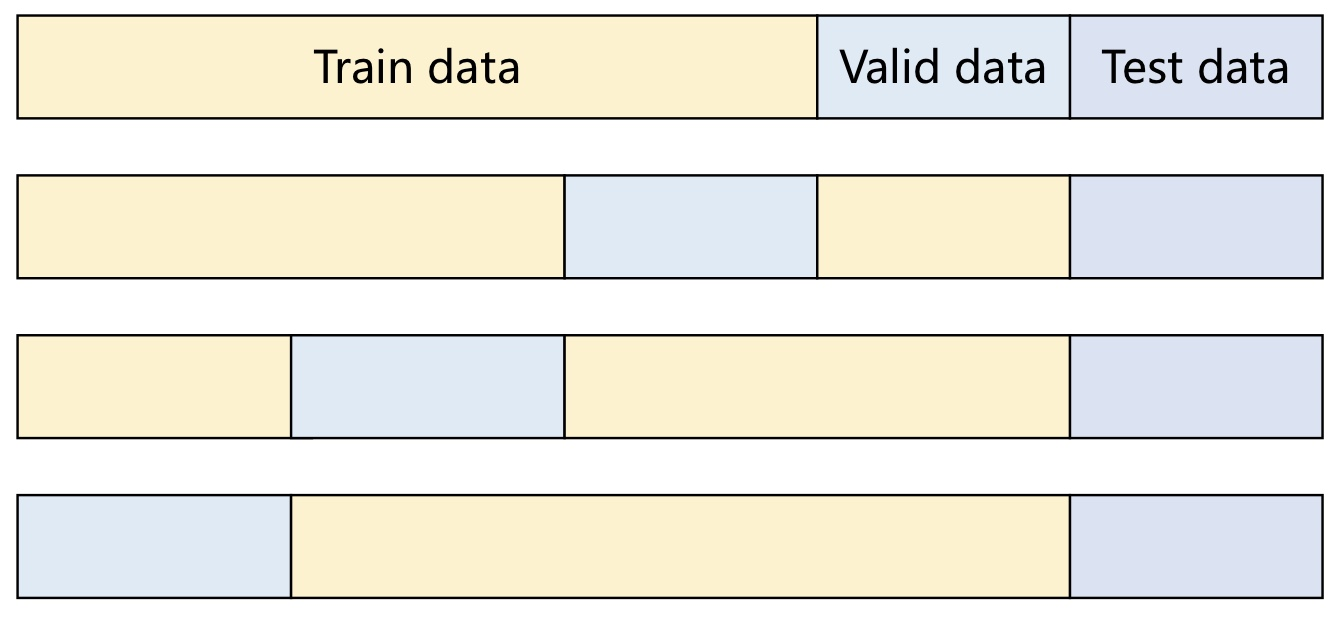
# K-fold cross validation(교차검증) 방법론
- 계산량이 많은 LOOCV의 단점을 보완하기 위한 목적
- (사람이 입력) 학습데이터를 K개로 쪼개서 순서대로 검증하는 방식
- K값이 커질수록 학습데이터 수가 많아짐 → 편향(bias)는 내려가고, 분산(variance)는 올라가고, 계산비용도 올라간다.
2. 정규화 손실 함수
- 데이터가 아닌 모델의 계산을 통해 해결하는 경우
- 파라미터수가 많은 복잡한 모델을 이용할 수록 발생하는 과적합(over-fitting)을 방지하기 위함
- 중요한 파라미터만 학습하기 위해서, 필요없는 파라미터(가중치)를 0으로 만들어서 없애는 방법
- 이 때 사용하는 2가지 정규화 방식이 아래와 같다.
* λ (람다)는 사람이 정하는 하이퍼파라미터이고, 보통 0.0001처럼 매우 작은수로 입력된다고함.
# Lasso 회귀 (L1 regression)
- Norm에 절댓값을 이용하는 방법
- 모든 파라미터(가중치)의 절댓값의 합에 λ (람다)를 곱하여 MSE 값에 더해주는 방식
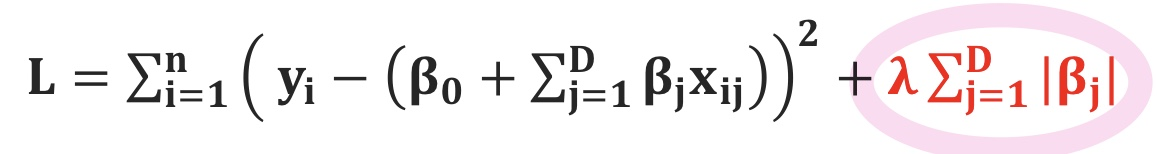
- 일차함수의 경우, 정규화 손실함수 그래프가 아래의 그림처럼 마름모의 형태가 나옴
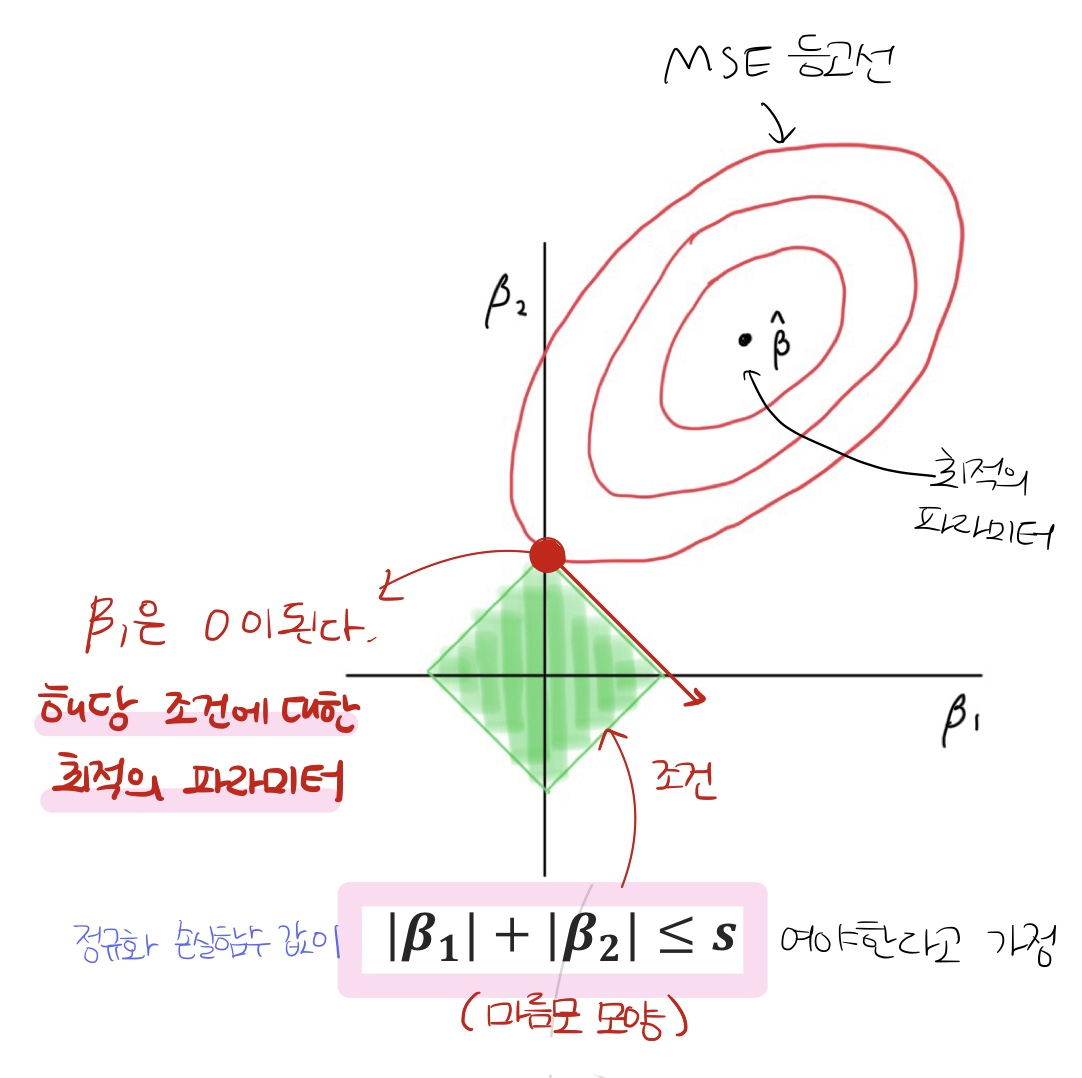
# Ridge 회귀 (L2 regression)
- Norm에 제곱값을 이용하는 방법
- 모든 파라미터(가중치)의 제곱값의 합에 λ (람다)를 곱하여 MSE 손실에 더해주는 방식
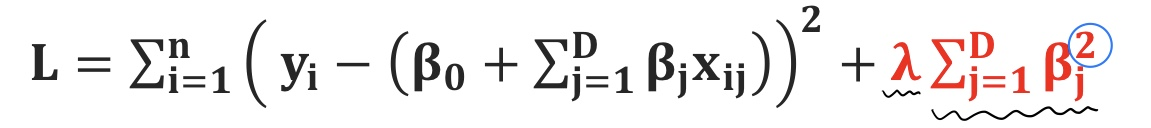
- 일차함수의 경우, 정규화 손실함수 그래프가 원의 형태로 나옴
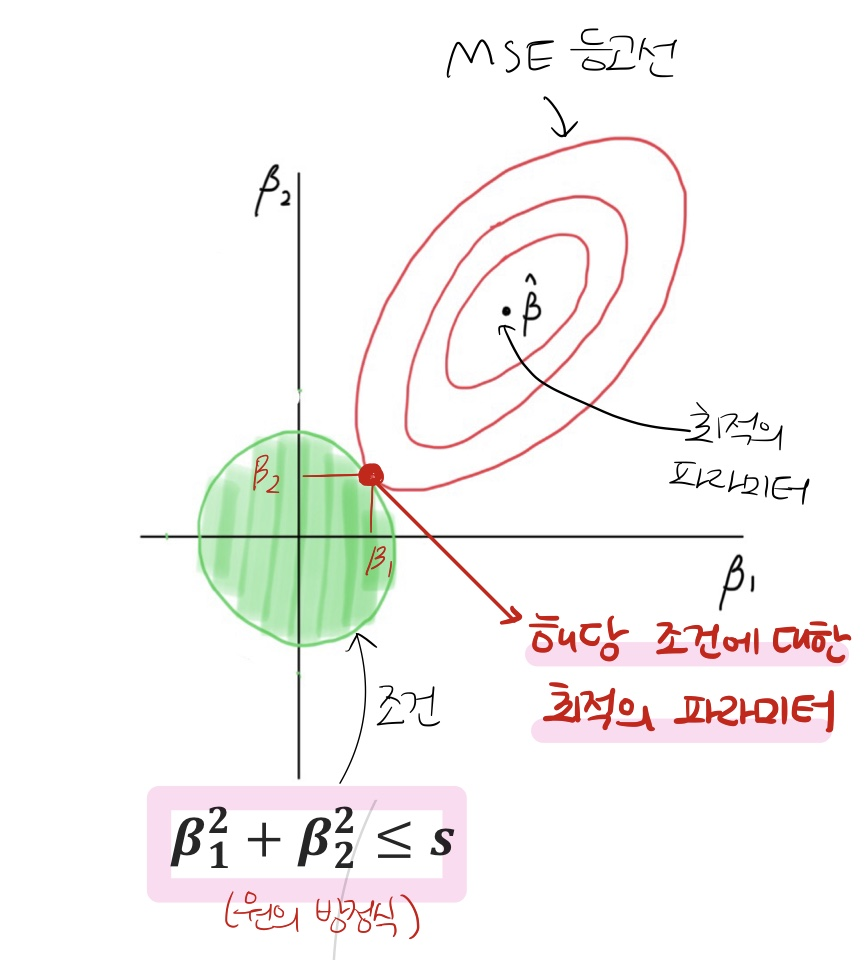
[Questions]
* 일반적으로 Ridge(L2 regression)을 많이 사용함
* 정규화에서 λ (람다) 값이 커질수록 손실값이 커지므로 파라미터수가 더 많이 걸러진다. = 모델이 간단해진다. = 편차(bias)는 높아지고, 분산(variance)은 커진다.
* 파라미터의 희소성(sparsity)은 Ridge < Lasso 이다. (Lasso는 무조건 0이 되는 파라미터가 있기 때문)
* 파라미터를 더 희소하게 만들기 위해서는 ① λ (람다) 값을 높힌다. ② 가중치에 대한 지수를 낮춰준다. (아래의 그림 참고)
[정리의 말씀]
머신러닝의 정확도를 높힐 수 있는 여러 방법론들이 있지만,
각 데이터와 모델에 따라 적용할 수 있는 방법론이 다르기 때문에
계산적인 요소뿐만 아니라 실험적 요소도 많이 고려해야 한다.