[칸아카데미] 모두를 위한 선형대수학 - (2) 벡터의 뺄셈, 단위 벡터, 직선의 매개변수 표현 정의 및 퀴즈

- 위치벡터(Standard Position Vector) : [0,0]이 벡터의 시작되는 지점(꼬리)인 벡터 (R2 기준)

- 단위 벡터(Unit Vector)
i (hat^) = [1,0] : 수평방향으로 1 이동하는 것을 의미
j (hat^) = [0,1] : 수직방향으로 1 이동하는 것을 의미

- 벡터의 표기법 3가지 (3번째 이미지 참고)
1) 열 벡터 (Column Vector)
2) 튜플 (Tuple)
3) 단위 벡터 (Unit Vector)

- 단위벡터 계산하는 법 (3번째 이미지 참고)
ex. v = (-2, 2)일 때, 각 열에 각 값의 제곱을 더한 값에 루트를 씌운 값으로 나누고, 그 각 열을 더한 값이 단위벡터이다.

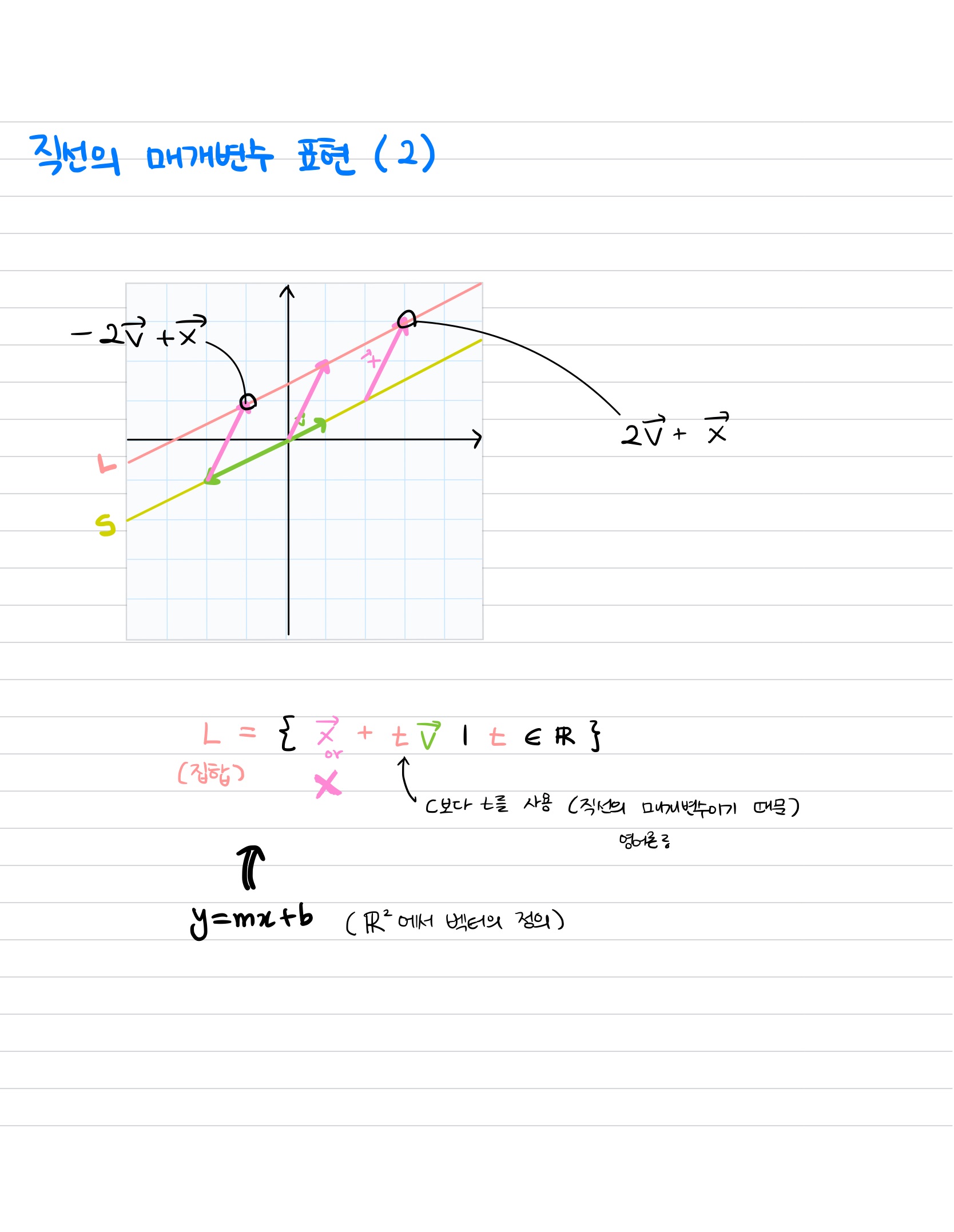
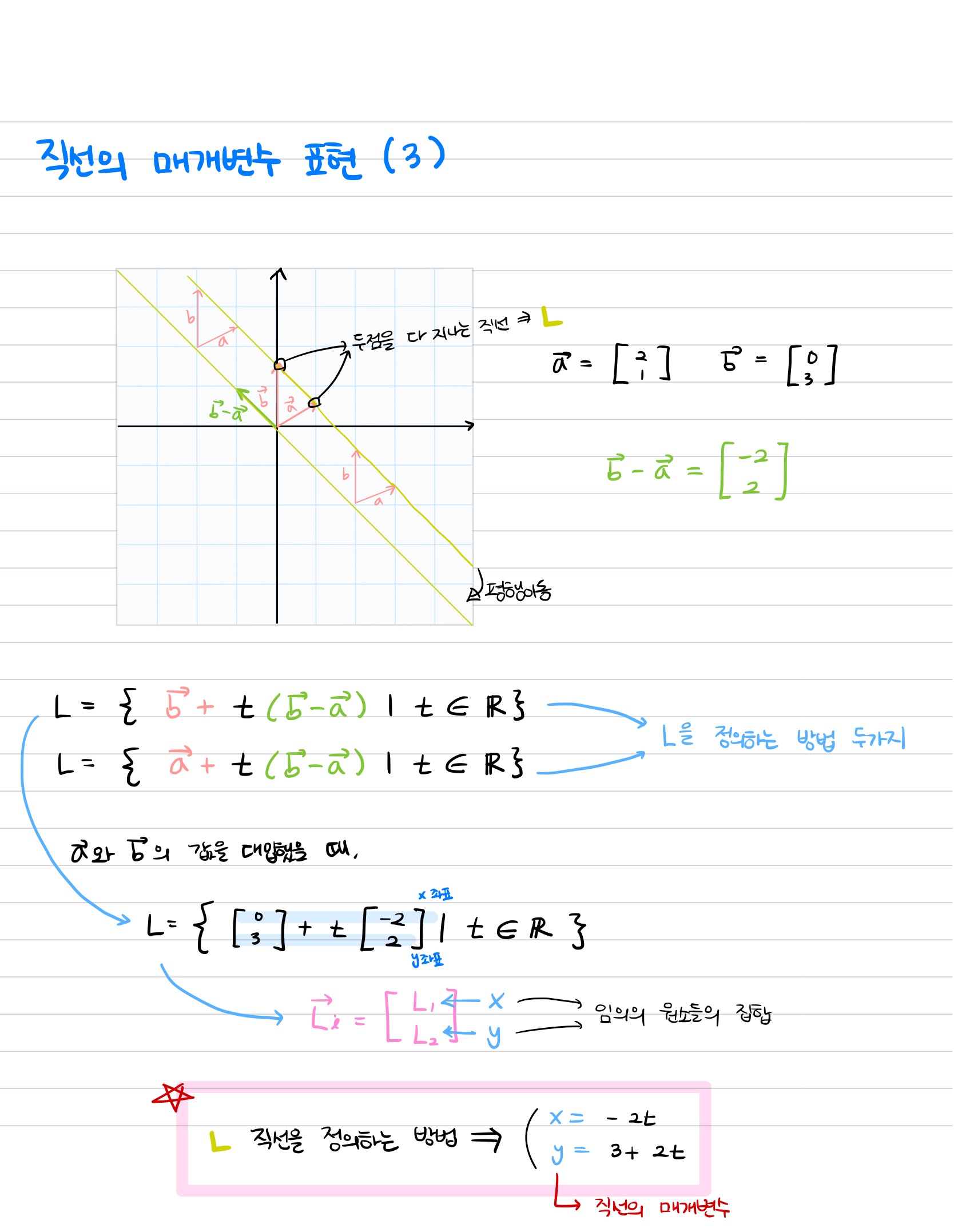
- 집합(Set) & 직선의 매개변수 표현 (4번째 마지막 그림 참고)
1) 벡터 v에 상수 c를 곱하는 것으로 만들 수 있는 모든 벡터의 집합을 구한다고 했을 때, 어떤 직선이 만들어 진다.
2) 이 직선에 모든 지점에 대해서 또다른 벡터x를 더할 경우, 또 다른 직선이 그어진다.
3) 이러한 과정을 식으로 표현한 것이 직선의 매개변수 표현이다.