지난 강의에서 공부했던 코시-슈바르츠 부등식 공식을 활용하여 삼각부등식을 증명할 수 있다.
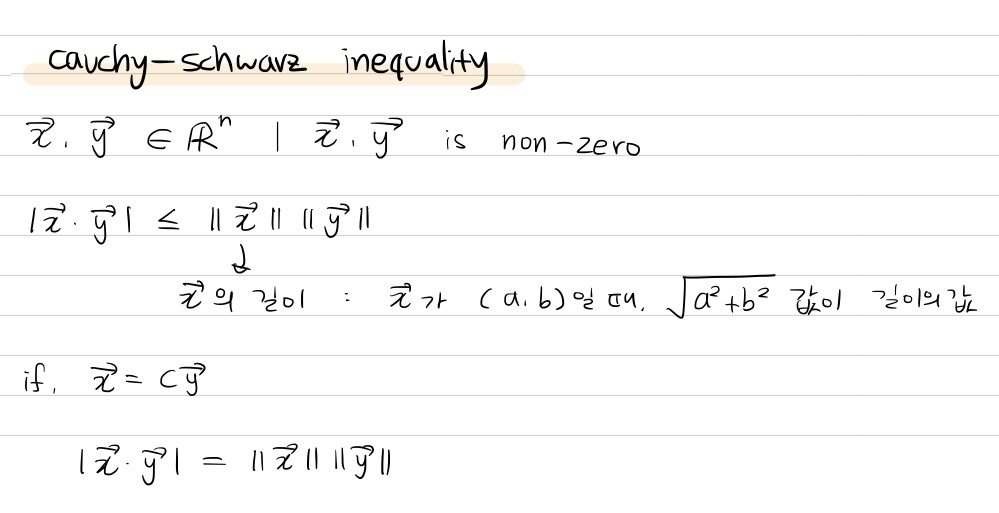
두 벡터의 합의 길이를 구하는 식에 위의 공식을 적용하면 아래의 보라색글씨의 공식이 나온다.
1) 두 벡터의 합의 길이는 항상 각 벡터의 길이의 합보다 작거나 같다.
2) 두 벡터가 서로 상수곱으로 구할 수 있는 벡터라면
두 벡터의 합의 길이와 각 벡터의 길이의 합의 값이 같다.
(단, 상수가 양수인 경우에만 해당됨)

'Mathematics > Linear Algebra' 카테고리의 다른 글
| [칸아카데미] 모두를 위한 선형대수학 - (12) 점과 법선벡터를 이용하여 R3에서 평면 정의하기 (0) | 2022.10.26 |
|---|---|
| [칸아카데미] 모두를 위한 선형대수학 - (11) 벡터 사이의 각 정의하기 (0) | 2022.10.14 |
| [칸아카데미] 모두를 위한 선형대수학 - (9) 코시-슈바르츠 부등식(Cauchy-Schwarz Inequality) (0) | 2022.09.28 |
| [칸아카데미] 모두를 위한 선형대수학 - (8) 벡터의 내적(Dot product)과 벡터의 길이(Length), 내적의 성질 (분배법칙, 교환법칙, 결합법칙) (0) | 2022.09.20 |
| [칸아카데미] 모두를 위한 선형대수학 - (7) 부분공간의 기저(a basis of subspace) (2) | 2022.09.18 |